This paper identifies fundamental processes behind urban design. Rules are derived from connective principles in complexity theory, pattern recognition, and artificial intelligence. Any urban setting can be decomposed into human activity nodes and their interconnections. The connections are then treated as a mathematical problem (here in a qualitative manner). Urban design is most successful when it establishes a certain number of connections between activity nodes. Mathematics itself depends upon establishing relationships between ideas; this ability being a central component of the intelligence of human beings. The creation of the built environment is driven by forces analogous to those that lead us to do mathematics.
Introduction
Architecture and urban design have so far resisted a scientific formulation in part because of their underlying complexity. The same reasons delayed the scientific foundations of medicine, which was until very recently based as much on superstition as on science. Efforts in the past to cast urban planning in theoretical terms -- by identifying the processes that give rise to observed forms -- have had little impact on actual development. There exist three notable and recent attempts: (1) the pioneering work of Christopher Alexander (Alexander, 1964; 1965; 1998; Alexander, Ishikawa et al., 1977; Alexander, Neis et al., 1987) provides the backbone for this paper; (2) the casting of urban patterns as fractals emphasizes their linked hierarchies and microstructure (Batty and Longley, 1994; Batty and Xie, 1996); (3) the formulation of urban questions in terms of relationships and movement sheds light on the forces governing the growth of a city (Hillier, 1996; Hillier and Hanson, 1984). Here, we will focus on connective processes as the basis of the urban web.
A central component of the human intellect is the ability to establish connections. Connections between ideas result in a better understanding of nature. Recognizing patterns that are hidden to the casual observer is the key to scientific development. Neurological studies show that most of the human brain is involved in visual perception, which suggests that intelligence has evolved to support the perceptual process (Fischler and Firschein, 1987). The ability to establish connections applies both to visual and to less obvious, more abstract processes, and it is by developing the latter that mankind has succeeded in dominating all other animal species. I will draw an analogy between mental connections, and connections among urban elements that give rise to a city or piece of urban landscape.
The urban web is a complex organizing structure that exists primarily in the space between buildings (Gehl, 1987). Each building encloses and shelters one or more human activity nodes. External nodes range from being totally exposed, to having various degrees of partial enclosure. The urban web consists of all exterior and connective elements such as pedestrian and green areas, free-standing walls, footpaths, and roads of increasing capacity from a bicycle path up to an expressway. Empirical observations verify that the stronger the connections, and the more substructure the web has, the more life a city has (Alexander, 1965; Gehl, 1987).
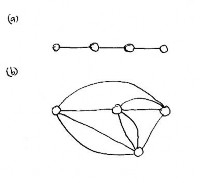
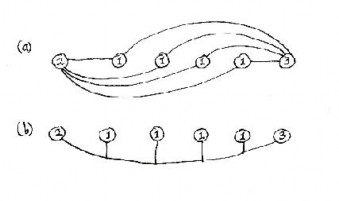
The exposition begins by stating three general principles. These are then developed into a theory of the urban web, which provides practical rules for applications. The need for different types of connections is discussed. A mathematical result on the irregularity of connections shows why straight paths that look regular on a plan are usually inadequate, and don't work for other reasons (Figure 1). A model used in molecular biology that pairs elements to achieve linkage is reviewed next. It demonstrates that the urban web cannot exist without a minimum (and very large) number of connections.
Next, how organized complexity is achieved in a city is examined. Not enough complexity, and a city is dead; if it has complexity without sufficient organization, a city becomes chaotic and unlivable. Raising the degree of organized complexity appears as one of mankind's fundamental drives throughout the ages. One of the principal ideas underlying this work is that a city mimics human thought processes, in that both depend on establishing connections. This analogy makes the underlying reasons for why we build complex things less mysterious.
The second half of this paper lists some applications of the theory. Roads and paths are the web connections, and we examine their piecewise structure and proper hierarchy. Hints and practical advice to planners are provided on how to build better neighborhoods. There are things that can be done to regenerate existing neighborhoods with minimal effort. How the success of a retail commercial area can be improved is mentioned. Finally, the proper use of boundaries is discussed. There exist many situations where one needs to inhibit or control connections instead of establishing them at all scales. In a healthy city it is necessary to disconnect two regions that will damage one another.
Structural principles of the urban web
The processes that generate the urban web can be summarized in terms of three principles. Though not exhaustive, they are entirely general, and this paper will describe how they translate into practical design rules for specific situations. Everything has to do with connections, and the topology of those connections. The three principles may be stated as follows:
-
Nodes. The urban web is anchored at nodes of human activity whose interconnections make up the web. There exist distinct types of nodes: home, work, park, store, restaurant, church, etc. Natural and architectural elements serve to reinforce human activity nodes and their connective paths. The web determines the spacing and plan of buildings, not vice-versa. Nodes that are too far apart cannot be connected by a pedestrian path.
-
Connections. Pairwise connections form between complementary nodes, not like nodes. Pedestrian paths consist of short straight pieces between nodes; no section should exceed a certain maximum length. To accommodate multiple connections between two points, some paths must necessarily be curved or irregular. Too many connections that coincide overload the channel's capacity. Successful paths are defined by the edge between contrasting planar regions, and form along boundaries.
-
Hierarchy. When allowed to do so, the urban web self-organizes by creating an ordered hierarchy of connections on several different levels of scale. It becomes multiply connected but not chaotic. The organization process follow a strict order: starting from the smallest scales (footpaths), and progressing up to the higher scales (roads of increasing capacity). If any connective level is missing, the web is pathological. A hierarchy can rarely be established all at once.
These principles are suggested by results in mathematics. The terms are not new (Lynch, 1960), but their use here is more specific than in the work of previous authors. As a result, the conclusions are stronger, and the allowed solutions are more restricted. Urban growth has followed similar rules throughout most of history. Urban planning in this century, however, incorporates rules that are in many ways the opposite of the above principles. I will show how the adoption of arbitrary design styles, which contradict the relevant mathematical principles, destroys the urban web (Batty and Longley, 1994).
Connections in architecture and urban design
Architecture ties structural elements and spaces together to achieve cohesion. Connections in urban design link three distinct types of elements with each other: natural elements, human activity nodes, and architectural elements. Examples of natural elements include a riverbank, a group of trees, a large boulder, or a patch of grass. Human activities define nodes such as a workplace, a residence, a storefront, or a spot to sit and drink a cup of coffee. Architectural elements include everything that humans build to connect natural elements and reinforce their activity nodes.
Connecting nodes of human activity
Urban nodes are not entirely defined by structures such as a prominent building or a monument. They can be more fleeting or modest, such as a hot-dog stand or a shaded bench. Nodes have to attract people for some reason, so a building or monument will mark a node only if there is a well-defined activity there as well. Prominent buildings and monuments that also provide a node for human activities act as a focus for paths, and succeed. By contrast, architectural sites that do not reinforce human activity are unsuccessful, isolating themselves from the urban web.
A distinction needs to be drawn between visual connections, and paths that connect the physical movement of persons. As emphasized by Kevin Lynch (1960), and developed later by Bill Hillier (Hillier, 1996; Hillier and Hanson, 1984), visual connections are necessary for orientation, and for creating a coherent picture of an urban setting. Nevertheless, because they do not always coincide with paths and roads, they are not the primary focus of this paper. The interdependence between visual connections and paths is highly complex, and will be treated elsewhere.
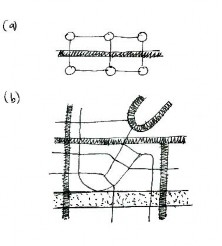
The number and types of connections between human activity nodes is (or should be) incredibly large. Since the 1940s, urban planners have followed rules whose aim is to create a plan with a high degree of geometrical regularity, at least in the urban core (Alexander, 1965; Batty and Longley, 1994; Gehl, 1987). This is often based on arbitrary stylistic ideas that frustrate both nodes and connections. By concentrating on the visual simplicity of overall forms, the human nodes are ignored until it is too late to define them properly. As a result, human activities have to fit into a pre-existing built matrix that can never hope to accommodate them (see Figure 1).
Architectural elements connect to each other at a distance visually through symmetries, similarity, and intermediate forms (Salingaros, 1995). There is a basic difference between architectural and human connections, however. Functional connections between human activity nodes are not amenable to a treatment in terms of symmetries, because those patterns are highly complex. For this reason, they tend to be ignored whenever a building or city is planned in visual terms. It is the organized complexity of a functioning urban web that determines its overall form, and not the other way around (see Figure 1). Organization combines multiple connectivity with a hierarchical ordering. A piece of the urban web may look organized but be disconnected. Conversely, another piece may look disorganized on plan, yet be highly connected and functional.
Connective paths are multiple and irregular
Every element in an urban setting has a meaning insofar as it relates to human activities. A complex process of organization connects the different nodes of the urban web. Connections enable one to get easily to any point, preferably by many different paths; what the neighborhood looks like to airplane passengers is largely irrelevant. An ordered urban environment that is strongly connected usually looks irregular from the air (Gehl, 1987; Hillier, 1996) (Figures 1 and 2). Geometrical regularity in the plan, while useful as an organizing principle, is not necessarily experienced on the ground (Batty and Longley, 1994).
A mathematical theorem says that two points can be connected by a straight line in only one way, but they can be connected by curved lines in an infinite number of ways. As we want the maximum possible number of connections between urban nodes, we cannot insist on straight connections on a Cartesian (Hippodamian) grid. As argued by Camillo Sitte, and verified by any observer, the curved streets of medieval towns give the greatest pleasure. This result is mimicked in modern suburban developments with curving streets, but those recent examples have insufficient internal and external connections.
The modernist idea of separating functions has been carried through to distinguish urban from suburban regions by means of opposite (and arbitrary) stylistic appearances. Geometrical regularity is the rule in urban regions. The opposite style has been applied to suburban areas. In the 1960s it became fashionable to build housing developments with curved streets. Connections are greatly reduced by having looped streets and cul-de-sacs. This approach has as its goal the isolation of nodes, which prevents the urban web from forming. We have imitated a superficial visual style here (the irregularity of medieval town plans) while failing to understand and reproduce the substance of the original solution (a high degree of pedestrian connectivity).
The theory of multiple connectivity is motivated and supported by a major result in physics. In Feynman's path-integral formulation of quantum mechanics, the interaction between two objects can be written as the sum of interactions over all possible paths. To compute the total interaction strength, one considers all possible paths linking two points, with appropriate weight according to their probability of occurrence. One then integrates along all of those paths to obtain the total interaction strength. By analogy, if we want every node in the urban web to be strongly connected, that is possible only via a multiplicity of irregular paths. (The Tokyo subway provides an example of many networks layered on top of each other).
It is neither necessary nor desirable to have all curved streets, however. There is in principle nothing wrong with a rectangular grid plan, and it has obvious organizational advantages. We criticize the rigidity of its most common application, which frequently limits the number of connections. It is possible to superimpose another grid at an angle to create diagonals; this will provide multiple connectivity. As illustrated later in this paper, one must allow paths to crisscross a rectangular road grid.
One could retain the clarity of a rectangular grid, and decrease the fineness of its subdivisions. Cutting into the rectangular grid with more parallel paths (vehicular or pedestrian) creates cross-connections, and if they are vehicular, that decreases the block size. Today, large city and suburban blocks frustrate cross-connectivity by not permitting internal paths. In the case of large commercial, residential, or government building complexes, it is necessary to cut paths through each group, otherwise that region will be isolated from the urban web. Large parking lots are pedestrian no-man's land, so paths there must be protected by raised pavements and canopies. Individual connections across an urban region will be composed of many smaller segments, and be multiple and irregular.
Stability against loss of connections
The suggestion may be made that complex workable cities are those which have a large degree of redundancy using the network concept. As you get more and more ways of traversing the city through its nodes, then if you sever a link between two nodes, the city still works. This is like the brain (Fischler and Firschein, 1987). If you lose some connections (either through injury, surgical intervention, or as a result of natural ageing), brains still largely work. That is because they have so much redundancy that messages still get through. Contrast this with machines that stop working entirely when a minor circuit is damaged. This notion of stability against cutting the network is complementary to the later idea of a threshold for complexity. Research already exists on the stability of communication networks where each line has a certain probability of failing, which applies directly to the urban web.
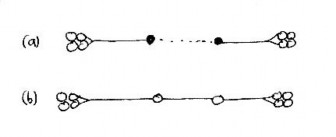
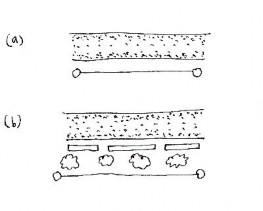
Avoiding channel overload
There are functional reasons for multiple connectivity. Often too many paths coalesce into one channel (see Figure 2). When the connections are all of the same type, they compete with each other and exceed the channel's capacity of flow. The singularity (a mathematical quantity that becomes infinite) manifests itself as either a pedestrian or a vehicular traffic jam. In instances where connections of different types coincide, the weaker connections disappear altogether. For example, pedestrian or bicycle paths cannot coexist with a highway. Connections on widely different levels can crisscross but not coincide.
The "toy model" from evolutionary biology
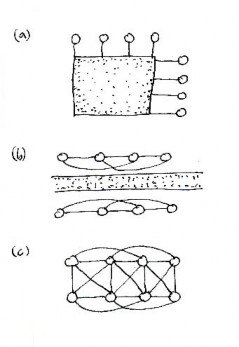
The new science of complexity supports our proposals for urban design. A result from random graph theory applied to a model in evolutionary biology illustrates what actually happens in creating an organized urban web. It mimics the process of building in history. Let us proceed to connect all the different elements in an urban situation. We try to achieve maximum organization by making adjustments to the components: moving them around, and modifying them so that nodes and architectural elements connect to each other at a distance. The goal is always to establish connections.
Organization can be studied in terms of pairwise linking. Consider N elements that are initially independent. Pick any pair at random and connect them, repeating this process at every step. Each time, one link is established, and in this way many small chains are created. The length of the largest chain initially will be very small, and grows slowly. At some point two or more chains will link. Up to N/2 steps, elements are linked largely into pairs that are independent of each other. When the number of pairwise connections exceeds N/2 , however, small chains begin to connect into larger chains, and at some point between N/2 and (N/2)lnN steps, many elements will link together to form one giant multiply-linked chain (Bollobás, 1985; Kauffman, 1995) (Figure 3). The larger the system, the more sudden this coalescence. The system has undergone a phase transition from a disorganized into an organized state. Further pairwise coupling will increase the size of this largest chain, but only by small increments, since it may already connect more than 80% of the elements (Bollobás, 1985; Kauffman, 1995).
This result applies to urban design in the following way. The planning process can either be mimicked with a computer model, or it is carried out gradually in actual building over the years. Connecting nodes incrementally will result in a perceptible improvement in the organization of the overall structure. What is seen is striking and is akin to a phase transition. A certain point is reached when almost everything coalesces: organization has been achieved. From this point on, every observer will experience the ensemble as being linked together.
A phase transition in complexity occurs; for cities, as the number of connections between distinct nodes/places passes a certain order, then a very large proportion of all nodes become connected suddenly. This explanation can be used for classifying cities and certainly idealized cities and their geometry, and it may even be linked to the performance of cities. This model of course is like a percolation model used for water flow: when enough holes appear in a porous medium, suddenly water passes through the material. Similarly, when enough trees are linked to form a forest, then a forest fire will spread throughout the forest. There exist quantitative results on this phase transition between slow and rapid flow.
Organized complexity versus empty purity
Architecture and urban planning can be understood as processes that (ought to) increase the degree of organized complexity. Much has been written about the organization of complexity, especially from the biological point of view (Kauffman, 1995; Simon, 1962). Different processes occurring together generate complexity; and if these are organized coherently, they result in organized complexity (Weaver, 1948). Where very few processes are occurring the situation is not complex to begin with. If, on the other hand, there is complexity but it is unorganized, then we are faced with a chaotic situation. That state is incomprehensible to the human mind, because it escapes our perceptive abilities (Simon, 1962).
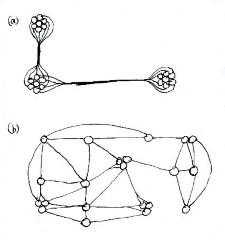
Mankind has always striven to increase the organized complexity of its surroundings, in parallel with a developing intelligence and improved grasp of natural systems. This century has seen a deliberate reversal of the process. Architects and urban planners became infatuated with visual simplicity and ignored the fundamental process of organization, which is not visually simple. We now have many examples of urban regions where the complexity has been eliminated altogether by suppressing connections (Batty and Longley, 1994). The search for visual purity in the plan has severely curtailed human activities that led to urbanization in the first place (Figure 4).
The principal model for twentieth-century planning, the Ville Radieuse, does not permit the connections that form the urban web. That model allows only pairwise connections between home and workplace, and no others (see Figure 4). What we have is a singular bundle of connected node pairs that do not interact. This is equally true between office blocks and high-rise apartment buildings, as it is between factories and suburban tract houses: the underlying pattern is disconnected. The number of pairwise connections equals N/2 , which is the threshold before the "toy model" previously discussed begins to connect internally. A fully connected graph needs the far greater number of (N - 1)N/2 connections. The necessary linkage for sustaining human life and activities is deliberately avoided in the Ville Radieuse.
Kevin Lynch introduced the mental image of a city as a means for judging its success (Lynch, 1960). Bill Hillier emphasizes the intelligibility of a city as the ease with which one perceives the path structure (Hillier, 1996). Here one may point out the crucial connection between hierarchical organization and simplification. A chaotic process is simplified by organization without necessarily losing any of its intrinsic content. Complex and diverse elements are grouped together so that they cooperate, and as a result they appear streamlined. By contrast, purification is a reducing process that loses much of the information inherent in a system. It is unfortunately very easy to confuse the two, with catastrophic consequences.
We now know much more about the perceptive processes that map the urban web onto the human mind. The two are very much alike, and consist of interacting connective nets on several different levels. An idea, or a path, is established by linking nearby strands of the network. The necessity of having many alternative paths, and comparing them, is the key to reasoned thought. We can be forced into one unique path by a planner, but that is not the way our mind works; it is how a robot functions (Fischler and Firschein, 1987). The quest for artificial intelligence in machines corresponds precisely in trying to go from mindless simplicity to organized complexity.
The degree of organization of any complex system depends directly on the ratio between the number of connections and the number of nodes. The following comparison is instructive. In conventional digital computers, the number of connections is comparable to the number of nodes (transistors), which is roughly that found in a minimal connected graph. In a brain, however, the number of connections is some four orders of magnitude (i.e., 10,000 times) larger than the number of nodes (nerve cells). Multiply-connected neural computers, which are successful in pattern recognition, are somewhere in-between. The mind-web analogy reveals just how enormous the density of connections must be in a successful urban setting.
Some applications of the theory
The remainder of this paper discusses practical situations. The three principles give rise to rules that suggest new techniques for building better neighborhoods. These are applicable to urban planning on all scales. There are things that can be done to regenerate existing neighborhoods. Altering and adding connections can drastically improve how a region works. Fairly complete details for specific solutions are already contained in the works of Alexander and his collaborators (Alexander, 1998; Alexander, Ishikawa et al., 1977; Alexander, Neis et al., 1987), Gehl (1987), and Greenberg (1995). Theoretical support comes from the research results of Batty (Batty and Longley, 1994) and Hillier (Hillier, 1996; Hillier and Hanson, 1984), and their collaborators. Here, we show how the solutions follow from the theoretical discussion in the first part of the paper.
Paths connect complementary nodes
So many well-meaning urban planners draw in footpaths on their designs that are never used in practice. They then conclude that people no longer wish to walk, and the next round of building eliminates the paths, now judged to be irrelevant. Yet around the world, in older cities and suburbs, and in regions that have not been destroyed by insensitive planning, people prefer to walk, not only for recreation and exercise, but for their daily routines. Incredibly, planners have forgotten humanity's basic means of locomotion, and are now frustrating it by means of built structures.
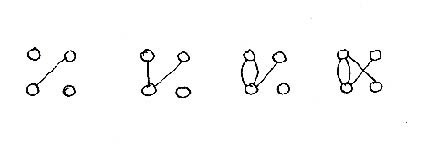
I have put off discussing until now the reasons why planned paths are seldom functional. First is the connective process itself: in general, connections will occur only between contrasting or complementary nodes. This follows from a basic law in architecture (Salingaros, 1995), which itself rests on fundamental physical principles (Figure 5). Electrical or fluid flow occurs only between points of differing potential. The urban web is created by the need to go from home to a school, a store, an office, or a park; there is much less need to go from one house to another. One's "closest" friends usually reside in several different neighborhoods, and don't coincide with one's immediate neighbors.
The neighborhood works only if contrasting nodes are placed so as to provide active links between like nodes (see Figure 5). This is the key to constructing the urban web: multiple connections are established between complementary nodes, then amalgamated into paths that also connect like nodes. By contrast, connections only between like nodes are just too weak to form a path. This is the main reason why suburbs are dead. We need a balance between like and opposite nodes. In amalgamating multiple connections into one path, care has to be taken not to overload the channel, but this is a concern only in high-density situations (see Figures 2 and 4).
Without a sufficient density and variety of nodes, functional paths (as opposed to unused ones that are purely decorative) can never form. Here we come up against the segregation and concentration of functions that has destroyed the urban web in our times (see Figure 4). There are simply not enough different types of nodes in any homogeneous urban region to form a web. Even where possibilities exist, the connections are usually blocked off by misguided zoning laws. Distinct types of elements, such as residential, commercial, and natural, must intertwine to catalyze the connective process (Alexander, Ishikawa et al., 1977). Dysfunctional cities concentrate nodes of the same type, whereas functional cities concentrate coupled pairs of contrasting nodes.
Paradoxically, connections occurring only between complementary nodes happens to be the assumption under which modern suburban planning operates. Nevertheless, this principle has been totally misapplied by today's planners who think strictly of automotive trips, and ignore the far more important pedestrian connections. The hierarchical ordering of different path types is crucial to creating the web of connections, and will be analyzed in the following sections. By reversing the relative importance of short versus long paths, all the other connections in the urban web -- those not involving a car, and the links between cars and pedestrians -- have been violated in modern suburban developments.
Human scales and piecewise connections
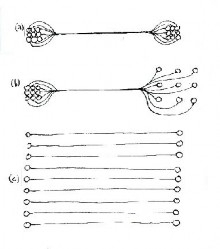
Pedestrians require a certain limited range of scales, outside of which they cannot function (Gehl, 1987). For example, people will not walk farther than a maximum distance between nodes (which can be determined empirically). This means that all useful pedestrian paths are connected piecewise: they are continuous but not smooth (Figure 6). Large plazas fail because they normally include footpaths that are too long; in most cases, those paths are also exposed or ill-defined, making them even less functional. Suburbia in general lacks paths of sufficiently short distance between nodes to create a web.
A mathematical result establishes the shape of individual path segments: the shortest distance between two points is a straight line. Pedestrians will therefore go from one node to another along the straightest possible line, avoiding corners, stairs, and changes of level (Gehl, 1987). This result applies only to the smallest scale. As discussed earlier, the need to have multiple paths requires that on the large scale paths are curved and irregular. There is no contradiction, for the two are related by another mathematical result: any global curve is locally straight in the limit of small measure.
The entire planning process actually follows from defining a proper pedestrian connection between two activity nodes. If they happen to be too far apart we have to introduce additional nodes at intermediate distances, otherwise this connection will not work (see Figure 6). Nodes need to be connected: this creates paths, which in turn create the need for other nodes. These new, intermediate nodes need to be connected to existing nearby nodes, requiring new paths, etc. In this way, the urban web generates itself. The more coherent substructure it has, the more stable it is.
Hierarchy and fractals
If we look at a successful city from the air, the picture is obviously fractal (Batty and Longley, 1994). This is not just a visual coincidence; Michael Batty and his group have derived rigorously the essential fractal nature of the urban web (Batty and Xie, 1996). By contrast, a picture of an artificial, dead city looks highly regular in plan, and has no small-scale structure. What we see in the first instance is a hierarchy of networks, all interrelated, and on different scales, from an expressway down to footpaths. The small- scale structure is what eventually guarantees the human liveability of a city; the large- scale connections facilitate movement on a much higher scale.
Hillier and his collaborators (Hillier, 1996; Hillier and Hanson, 1984) have run computer simulations on how urban form is generated. Among the many results obtained that are relevant to this issue, one overwhelming fact emerges: the spatial structure of cities is the disorderly outcome of a long history of small-scale incremental changes. The resulting patterns have neither geometrical nor functional simplicity. The design of the global object -- the city -- emerges of its own accord from a locally ordered system. While I will not review those results here, they underline the importance of beginning with a small scale, and allowing it to evolve so as to influence the larger scales.
The success of retail areas and plazas
Mike Greenberg, a keen observer of urban situations, analyzes the role connections play in the success of retail areas (Greenberg, 1995). The nature of pedestrian paths establishes a maximum but not a minimum length for each segment. The more segmented a path is (by virtue of having more intermediate nodes) the stronger and tighter the web structure. Older commercial streets provide nodes (stores) next to each other. The variety and proximity of stores allows them to be linked into a retail district. Large indoor malls go one step further and also provide short connections between opposite facing storefronts, which is not in general possible across a downtown street (Greenberg, 1995) (Figure 7).
The same solution applies to a successful plaza. A pedestrian zone is not created by simply banning vehicular traffic; it is defined by an overlapping and crisscrossing of pedestrian paths. Pedestrianization is advisable if it is impossible to define just one or two paths to accommodate all the pedestrian connections. As argued above, different paths must link complementary points of interest. A plaza that works is defined by having opposite types of nodes all around it. If there is no traffic to impede a pedestrian, and if all possible paths nearly cover an area, then it is better to make it a pedestrian zone rather than to create many separate paths.
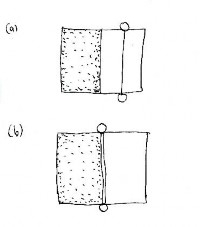
A path as the edge of a region
Paths are linear mathematical elements defined by the differentiation between contrasting or distinct regions. A path through a uniform area is ambiguous, because it divides the area into similar components on either side; it could just as well be placed anywhere inside that area. (Note that a multiplicity of well-defined paths is the opposite of an ambiguity in defining a single path). A path succeeds only if it coincides with the boundary of an area such as the edge of a building (Gehl, 1987), thus combining in an essential manner two of Lynch's urban elements: path and edge (Lynch, 1960) (Figure 8). In the absence of an existing edge, a wall creates a division along which a path can develop. Whereas Lynch noted that sometimes paths develop along edges, we insist that paths and edges are potentially one unit. In graph theory, which we propose as a means of understanding the urban web, paths and edges are the same thing.
Maximal stability requires every element of the urban web to reinforce every other element. Otherwise, forces are generated that will unbalance or disrupt the design. From the point of view of an area being divided, a path disturbs the original unity of that area; it is an intrusion, and is therefore unsupported by the area itself. It is very different when a path is created along a boundary between two distinct areas. The path now supports the boundary, and vice-versa. An architectural law defines units via contrast (Salingaros, 1995): any division must be into a complementary pair, not a similar pair.
Additional psychological data reinforce this property of paths. People do not feel comfortable walking through the middle of spaces, with the same environment (either open and unprotected, or walled-in) on both sides (Gehl, 1987). This is an expression of subconscious feelings of being protected from danger; one wants to be next to something solid, facing outwards. Paths need to be protected by an edge. That is the reason why a chain-link fence is no substitute for a wall, and also why huge parking lots are so dehumanizing. The other extreme, where a path is walled-in on both sides, is claustrophobic. A plaza works best if it provides a substantial edge surrounding its multiple paths.
Priority for creating pedestrian paths
The urban web consists of overlapping networks of connections. There is no reason to suppose, as many planners do, that the distinct networks have to coincide. Different types of connections exist on different scales, so mathematically they cannot coincide. The web has structural strength only when networks on different levels cross and overlap, providing cross-connectivity. When connections are forced to coincide they become singular (too many are concentrated along one path). Singular connections do not work because they overload the carrying capacity of the channel (see Figures 2 and 4).
The number of pedestrian paths in the urban web should be far greater than exists today. An unfortunate trend of the last 70 years has been to eliminate footpaths by arbitrarily imposing a rectangular (or other restrictive) road grid for all connections (Batty and Longley, 1994). A second error has been to give priority to car paths over pedestrian paths. Alexander and his associates have looked into the process of establishing the web connections (Alexander, Neis et al., 1987). They conclude that there is an optimal sequence to be followed: define the pedestrian and green spaces first, followed by pedestrian connections, buildings, and roads, in that order (Alexander, Neis et al., 1987). The greatest cities of the past were built by following the order proposed here. A careful study of the urban web clearly shows that following the reverse order, as is done today, eliminates pedestrian and usable green areas.
The nodes of a neighborhood must be connected by functional footpaths. Today this occurs only in some of the older (pre-1940s) neighborhoods. Clusters of houses should also be connected by bicycle paths. By this we do not necessarily mean the separate paved variety, but a reliable way to ride a bicycle without getting off, or endangering yourself on a busy street. (This concept is due to Greenberg (1995)). When clusters of houses are connected only by a local road, pedestrian and bicycle connections are neglected. In most cases, moreover, the road is not strictly local but doubles as a busy two-way through road, which makes the situation worse.
Footpaths need not be necessarily distinct and separate from bicycle paths. Nor are these necessarily distinct and separate from streets; it all depends on traffic density. Indeed, pedestrians crave the visual connection that a footpath along a street affords. This is also a requirement for increased safety, as isolated footpaths can be dangerous. As long as the traffic flow is not uncomfortably large a footpath can run parallel and next to a street. With appropriate slowing-down devices, footpaths can even coincide with vehicular streets (Gehl, 1987).
Guaranteeing the functionality of individual paths
The preceding parts of this paper talk about establishing as many paths as possible to connect nodes in the urban web. There is a limit to this process, however. As in all natural connected systems, we wish to establish only those connections that work; that are truly necessary for multiple connectivity. Some guidelines have been given that help to judge whether a connection is likely to be used or not. We wish to avoid connections that are not used for whatever reason, including factors beyond those discussed here. For example, decreasing the block size -- a commonly proposed urban solution -- does not always guarantee that newly-created cross streets will be used by sufficient traffic. This is needed to justify their additional expense, and also to offer safety from crime (Hillier and Hanson, 1984).
In another situation, when the city fights for public right-of-way across a commercial lot, that path had better be used, otherwise the process will be discredited from future applications. The urban designer has to optimize conditions so that a given path will carry sufficient traffic to make it viable. Dysfunctional non-paths are the product of thinking in terms of geometrical regularities; in that mind set, paths are (wrongly) assumed to be created by some sort of visual symmetry on the plan. Even though the present model for the urban web frees us from this error in approach, only a short displacement distinguishes a path that works from one that doesn't, and this is not obvious on a plan. Nor are many of the other factors that influence the success of a path.
Some intelligent, perceptive people claim that the pedestrian city is dead, and could exist only under conditions that are no longer reproducible. I do not agree. The reason for their pessimism is that pedestrian paths no longer seem to work. I claim here that most paths today are artificial, decorative paths that cannot be made to work. They correspond to wrong lines on a sketch. In order to repair existing urban regions, we have to erase those wrong lines; i.e., get rid of or transpose paths that are of this useless, frustrating type. If it cannot be fixed, an existing non-path will certainly discourage the building of a functional path nearby, and so it poses an impediment to generating the urban web. In many regions, such non-paths have replaced the older type of useful paths, thus establishing a flawed pattern to be copied by contemporary urban planners.
The pattern of roads as an organizing principle
Vehicular traffic is meant to facilitate human activity. After the natural elements, architectural elements, and pedestrian connections are established, then roads are introduced to organize the connections on a higher level (Alexander, Neis et al., 1987; Greenberg, 1995) (Figure 9). It is essential to establish vehicular roads in the proper hierarchy. In any complex system, organization proceeds from the small to the large. Each type of road is meant for traffic of distinct densities, and one size cannot accommodate all of them. Several independent connective networks will have to intersect at many different points. Each type of intersection presents a special problem to be solved, otherwise the circulation will be interrupted (Alexander, Ishikawa et al., 1977; Greenberg, 1995). (Cross-over points will not be analyzed here).
Pedestrian paths cross and connect to a local street. (b) Local streets feed into a through street, with superimposed pedestrian and bicycle paths.
There is now a profusion of medium-density car roads that try to serve (with limited success) widely different traffic flows. Looped and cul-de-sac streets prevent through traffic in new suburban subdivisions. Their application is paradoxical, however, because it tries to reduce traffic flow while maintaining a road whose width and surface are appropriate for a highway (Gehl, 1987). This ignores and cuts the footpaths and bicycle paths, which can effectively cross only a genuinely low-capacity road. Also, the connective web must continue in all directions, so that if any road stops, pedestrian and bicycle traffic can continue on a path between houses. Foot and bicycle paths should constitute totally independent networks from local roads (Alexander, Ishikawa et al., 1977) (see Figure 9).
Here we come to a crucial observation from complex systems: hierarchical organization requires that components of different sizes fit properly into the whole. The pieces of the urban web are simple, and they interact in a simple manner; yet their union is highly complex. The method for putting them together has to respect this complexity (Alexander, 1964; 1965). We cannot solve the problems inherent in the organizational process on paper in a day. Hierarchical systems depend on the proper interaction of connected elements on many different levels, and necessarily require a dynamic process for their growth. Any simplistic attempt at organization is bound to miss many of the connections that contribute to internal stability.
The present model has not been developed into how the dynamics of streets and paths relates to the performance of cities. The interior logic of a city's disorderly grid is fundamentally about movement, so that many properties of urban space are a product of these connections (Hillier, 1996; Hillier and Hanson, 1984). A source of literature on space syntax -- starting from the work of Hillier and collaborators (Hillier, 1996; Hillier and Hanson, 1984) -- is the journal Environment and Planning B. That work tries to associate pedestrian and street networks to crime and congestion, especially in housing estates. In this context, traffic assignment models assign traffic from many origins and destinations to a much reduced set of paths, mirroring Figures 2 and 4. This simplification of the urban road grid often exacerbates the very problems that it tries to solve.
Necessary discontinuities and separation
Not every node in the web should be connected to each other. Taking the cue from biological systems, different organs would interfere with each other's function unless they are separated locally. Elements of the urban web can damage an adjoining element unless care is taken to insulate them. Examples are: an expressway next to an apartment complex, a footpath next to a highway, heavy industry next to houses, a slum next to an upscale area (Figure 10). All of these are necessary components of a city, and are usually isolated from each other by some sort of barrier (Alexander, Ishikawa et al., 1977). This is not a sociological statement, just an observation of what actually happens. Lynch (1960) emphasizes the important and necessary role of an edge as a boundary.
Highway is flanked by a low wall with gaps and trees, which protect the pedestrian and bicycle paths.
A sidewalk adjoining a busy highway is dangerous, so it is rarely used. It survives as an anachronistic remnant from small towns with low-speed traffic. No thought has been given lately to the interaction between pedestrians and cars. In this situation, a sidewalk should be insulated by a barrier: either sections of solid wall, or a wide green area with trees (see Figure 10). There is no need for connection (except perhaps a visual one) between pedestrians and high-speed traffic. Any road on which a car cannot stop to pick up or discharge a passenger is effectively isolated, and should be designed that way.
Disparate urban functions and neighborhoods tend to coexist in a more healthy balance when they have a barrier between them (Alexander, Ishikawa et al., 1977). We are not talking about separating commercial from residential areas, which have to intertwine, but rather the use of edges as constructive boundaries. High-density roads cut across the urban web effectively. Other solutions include a wall, a river, or a large park; all these are found in older cities. In new developments, rivers are covered over because they don't fit into the rectangular grid, thus wasting an excellent natural barrier. Oftentimes, an existing barrier has led to the differential growth of the areas on either side. In other instances, a boundary has provided long-term stability to a neighborhood.
We mention boundaries because they are now put up at all the wrong places. Mathematically, we still have only web nodes and connections. As pointed out earlier, walls are ideal for reinforcing paths and roads, but instead they are often used to block connections. A solid wall needs openings to allow paths through. Strong connective elements such as a highway will need to be introduced into a city at some point. Instead of being placed where a separation is needed, however, they invariably cut across and sever existing connections. Connective and insulating elements are complementary, and their misapplication for the opposite purpose is based on a misunderstanding of the urban web.
Local petty crime can also destroy the connections in neighborhoods that have, up to that point, been working fairly well. When the urban web is threatened, it reacts organically by building fences to protect itself, in analogy to a biological wound growing scar tissue. This single act reorganizes a neighborhood spatially, severing connections with what is perceived to be the source of crime. If that source is not localized, each node or group of nodes will isolate itself with a fence, thus tearing the urban web. A neighborhood can recover from some petty crime, but the web can never recover once connections are blocked.
Conclusion
This paper derived a set of planning principles from mathematical considerations, and summarized the connective processes that generate the urban web. The principles are satisfied by all successful urban environments around the world. On the other hand, they are violated by urban environments that fail, that are unfriendly, that are unpleasant, that are isolating, and that are dehumanizing. By applying zoning laws that violate basic connective needs, we are responsible for many of those failures. It is possible, however, to create our cities according to the appropriate mathematical principles behind human activities.
Maintaining a large variety of paths and green spaces is unavoidably costly. All indications, however, are that the cost to society is incomparably greater if these solutions are not implemented. A breakdown of the neighborhood leads to alienation and increased crime; followed by suburban flight and decreasing property values. In financial terms, the end result of trying to save on the bill for achieving a proper balance of urban elements could be to lose a major part of the area's tax revenue. In human terms, the result can be devastating. These ultimate costs have to be very carefully considered by urban planners.
Acknowledgments: This research has been supported in part by a grant from the Alfred P. Sloan Foundation. The author has profited from many stimulating discussions with Mike Greenberg.